1.1. Простейшие пространства событий и их
инварианты. Четырехвекторы
Начала математического формализма
Модели Мира
Согласно существующим представлениям взаимодействие между
объектами материального мира, не обладающими вращательными степенями свободы, может
быть изображено в четырехмерном пространстве событий
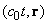, где
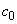- скорость света в квадрупольном
вакууме;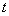 
- время, а
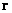- координата поступательного
движения.
Введем теперь понятие интервала, который используется
в специальной теории относительности.
С математической точки зрения интервал
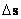есть промежуток между двумя
событиями, называемыми в четырехмерном пространстве-времени мировыми событиями.
Квадрат такого интервала между любыми двумя событиями А и Б, происходящими
в среде квадрупольного вакуума, равен
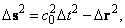(1.1.1)
где
,
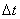- промежуток времени и пространственное
расстояние между этими событиями соответственно.
Что означает выражение (1.1.1)?
А тем самым мы выбрали геометрию пространства в нашей
модели. В частности, мы положили, что Мир четырехмерен, причем он содержит три пространственные
координаты и одну координату времени. Мы также приняли, что характерной
скоростью распространения энергии и информации в пространстве является скорость света.
Вместе с тем это не значит, что мы ограничили скорость распространения энергии и информации
скоростью света. Просто это в данном случае одна из фундаментальных и характерных параметров
Мира. Далее мы покажем, каким образом энергия и информация могут распространяться с
большими, нежели скорость света, скоростями.
Какую еще информацию содержит в себе выражение (1.1.1)?
Интервал инвариантен относительно Лоренц-преобразований,
то есть остается неизменным при переходе от одной системы отсчета к другой, хотя по
отдельности величины
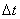и
от принятой системы отсчета
зависят.
Назовем пустую, то есть без дипольного вакуума, однородную,
изотропную и изохронную пространственную среду Х, как некоторое геометрическое
множество точек, таких, что
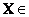r,
невозмущенной или просто пустым пространством, а время
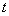- стандартным временем
в произвольной точке 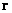данного
пространства или также невозмущенным. Такое пространство событий можно представить
в виде некоторой идеальной среды — невозмущенного квадрупольного вакуума. Этот
вакуум в данном случае называется абсолютным вакуумом.
Подчеркнем, что введенное пространство событий - всего лишь
абстрактное математическое представление, система координат, в которой рассматриваются
происходящие события.
Вместе с тем, по моему убеждению, реально существующий квадрупольный
вакуум - весьма сложная и динамичная среда. Поэтому в данном случае для обозначения
реальной динамичной среды, состоящей из квадриг Терлецкого, используется словосочетание
квадрупольный вакуум. Термин же абсолютный вакуум здесь
используется для обозначения предельного, то есть невозмущенного состояния квадрупольного
вакуума, что собственно и следует из внутреннего смысла данного словосочетания как
некоторой идеальной среды без внутренних возмущений и превращений, фактически
представляющей собой пустое пространство. (За исключением, быть может, определенных
точечных образований, состоящих из вещества или дипольного вакуума, при условии, что
они в рамках решающих задач не влияют сколько-нибудь заметно на исследуемые явления.)
После того как разобрались с исходными определениями, выделим
в произвольной точке среды или поместим в нее, как говорят физики,
пробное тело, то есть некоторый
объект. Это могут быть тела, занимающие малую область пространства, или небольшой фрагмент
самого пространства, которые по условиям решаемой задачи можно считать точечными.
В случае, когда в каждой точке пространства событий исследуемый
объект испытывает воздействие сил только одной физической природы, без ограничения
общности рассматриваемых эффектов считаем, что начальные временные и пространственные
координаты такого точечного тела или макрообъекта равны нулю. При этом
,
,
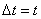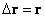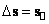, и левая часть (1.1.1),
являясь квадратом четырехмерного вектора
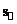, будет выглядеть следующим
образом:
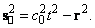(1.1.2)
Для последующей унификации и удобства мы в (1.1.2) и ниже
знаком "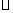
" обозначаем, что
соответствующий символ является четырехвектором.
В данном случае, параметр
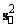является инвариантом, то
есть величиной, сохраняющейся, при преобразованиях от одной инерциальной системы отсчета
к любой другой. В этом случае можно считать, что он равняется квадрату некоторого числа
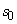, то есть
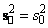. Тогда соотношение (1.1.2.)
можно записать в виде:
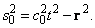(1.1.3)
С целью наглядности представления подобное пространство
событий обычно изображают для какой-нибудь одной пространственной координаты,
например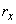 
, упрощая модель
и считая 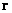не трехмерным вектором,
а одномерным, то есть просто скаляром
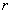. В последнем случае пространство
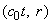является двумерным. Тогда
его можно достаточно просто представить зрительно и изобразить на листе бумаги (рис.
1.1.1).
Из рисунка видно, что это пространство имеет две принципиально
различные области, разделенные пунктирными прямыми
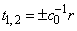. В области I (на рис. 1.1.1
она светлая), где квадрат интервала
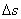положителен, то есть
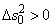, события называются времениподобными.
В этом случае известно, что прошлое каждого события влияет на его будущее. То есть
такие события, разнесенные пространством, могут физическим образом влиять друг на друга.
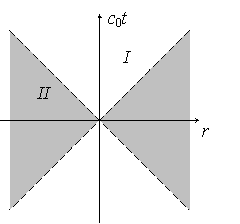
Рис. 1.1.1 Двумерное пространство событий материального мира.
В области II (на рис. 1.1.1 она затемнена) квадрат интервала
отрицателен, то есть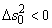 
. Такие
события называются пространственноподобными. Считается, что если эти события
разделены пространством, то они не могут физически влиять друг на друга.
Координаты
можно рассматривать как
компоненты четырехмерного радиус-вектора или просто 4-вектора точки в пространстве
событий.
То есть в данном случае четырехмерным вектором
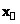называется совокупность
четырех величин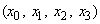 
, которые
при преобразованиях четырехмерной же системы координат изменяются таким образом, что
квадрат его «длины»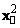 
определяется
из соотношения
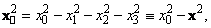(1.1.4)
где
,
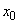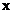- временной и пространственный
трехмерный компоненты данного 4-вектора соответственно.
Аналогично (1.1.4) вводятся понятия для двух разных 4-векторов
,
:
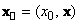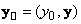- скалярного
произведения
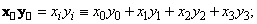(1.1.5)
-
векторного произведения
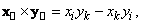(1.1.6)
где
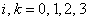, причем везде по дважды
повторяющимся индексам здесь и ниже подразумевается суммирование.
Теперь рассмотрим другие инварианты,
которые связаны с энергетическими взаимодействиями тел в пространстве событий.
Второй инвариант, который имеет
место при преобразованиях Лоренца, - квадрат обобщенного
4-импульса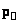 
произвольной
выделенной частицы, движущейся в пространстве событий:
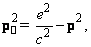(1.1.7)
где
,
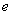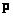- релятивистская энергия
и обычный трехмерный релятивистский импульс частицы соответственно; c - скорость
света в среде.
В данном случае для среды квадрупольного вакуума
c =
;
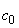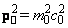, и сам инвариант (1.1.7)
выглядит следующим образом:
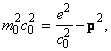(1.1.8)
где
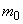- масса покоя частицы.
Другую группу инвариантов можно получить для замкнутых систем,
обладающих только вихревыми компонентами, но не участвующих в поступательном
движении. Они следующие:
- четырехмерный момент импульса частицы (сравните с (1.1.6))
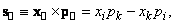(1.1.9)
где
,
.
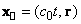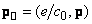Для осесимметричных систем (1.1.9) распадается на два инварианта:
- трехмерный механический момент количества движения частицы
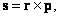(1.1.10)
а также - векторную величину
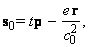(1.1.11)
связывающую временную и пространственную координаты частицы.
Приведем еще одно соотношение с размерностью действия, которое
для осесимметричных систем является комбинацией уже представленных выражений (1.1.3),
(1.1.8) и (1.1.11):
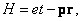(1.1.12)
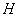- параметр с размерностью действия.
В случае, когда левая часть (1.1.12) является
константой, то есть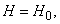 
данное
выражение можно записать следующим образом:
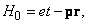(1.1.13)
где
.
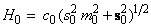Соотношения, подобные (1.1.3), (1.1.8)-(1.1.11), (1.1.13),
имеют место и для макрообъектов или ансамбля частиц, но так как никаких новых результатов
они не привносят, то будут приведены по мере необходимости в процессе дальнейшего изложения
материала. Здесь лишь отметим, что аналогичные инварианты, только для заряда, можно
получить, использовав аналогию между массами и зарядами. Для этого, подобно (1.1.8),
определим произведение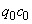 
как
инвариантную длину четырехмерного вектора - плотности токового 4-импульса или просто
плотности 4-тока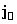 
, квадрат
которого равен
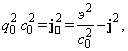(1.1.14)
где
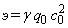- величина, имеющая размерность
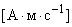, являющаяся для заряда своеобразным
аналогом релятивистской энергии;
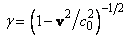- релятивистский фактор,
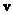- скорость частицы;
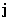- трехмерная релятивистская
величина плотности тока частиц;
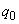- заряд неподвижной частицы.
Мы его также называем статическим зарядом частицы.
Из (1.1.8) и (1.1.14) следует, что инвариантные масса и заряд
действительны, если вектора
,
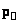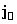времениподобны, то есть
,
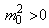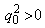. Если же эти
вектора пространственноподобны, то
,
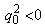. В последнем случае инвариантные
масса и заряд являются чисто мнимыми величинами.
Соответственно, для времениподобного интервала
;
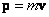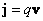, где
;
.
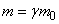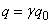В случае пространственноподобного интервала из этих же соотношений
следует, что скорость частиц будет больше скорости света
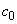, а соответствующие величины
станут мнимыми, то есть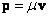 
;
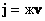, где
,
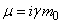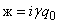- релятивистские заряд и
масса мнимых частиц.
Из всего этого можно заключить, что при скорости частиц
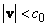происходит передача энергии
за счет поляризации проявленного вещества, а при
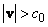- поляризации непроявленного
вещества, то есть при помощи соответствующих квазичастиц или, другими словами,
посредством изменений поляризации самой среды.
Для полноты картины выпишем другие инварианты, существующие
для заряда. Они будут аналогичны выражениям (1.1.9)-(1.1.11) и (1.1.13), и первое их
них - четырехмерное вихревое соотношение для заряда
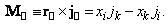(1.1.15)
Для осесимметричных систем (1.1.15) распадается на два инварианта:
- трехмерный вихревой «момент» для заряда, создающийся за
счет вихревого тока ,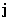
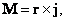(1.1.16)
-
векторную величину, сохраняющуюся
в осесимметричных системах,
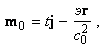(1.1.17)
где
,
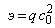- инвариант, аналогичный (1.1.13),
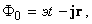(1.1.18)
где
.
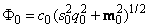Изменения массы и заряда, как параметров, удобно изобразить в
координатах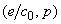 
, 
.
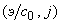Эти зависимости выглядят следующим образом.
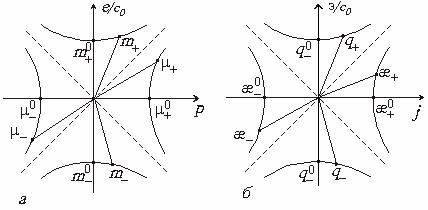
Рис. 1.1.2. Параметрические зависимости
(а) масс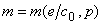 
и (б)
зарядов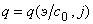 
как функции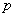 
и
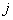соответственно.
Из последних рисунков видно, что пересечения соответствующих
гипербол, выделенных сплошными кривыми, с осями координат
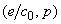и
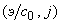определяют значения инвариантов
а) для масс:
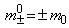, когда
,
;
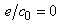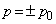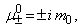когда
,
;
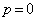б) и зарядов:
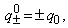когда
,
;
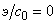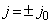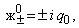когда
,
;
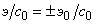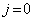где
,
,
.
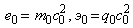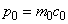Отрезки прямых, выходящие из начала координат и пересекающие
соответствующие ветви гипербол (рис. 1.1.2), характеризуют величины масс
,
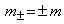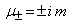и зарядов
,
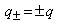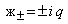при
,
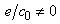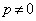и
,
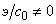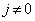соответственно.
Всего существует по восемь вариантов
а) для масс:
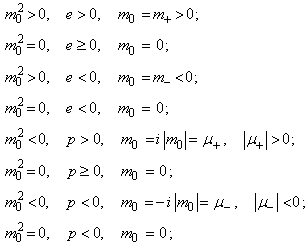(1.1.19)
б) и для зарядов:
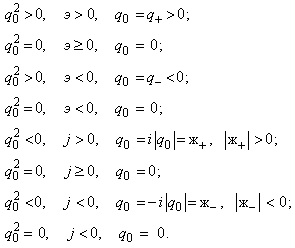(1.1.20)
Если исходить из представлений (1.1.19) и (1.1.20),
всего имеется по три вида масс и зарядов, имеющих реальные
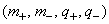, мнимые
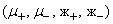и нулевые массы
и заряды, причем из-за различия в знаках каждый из этих видов содержит по два типа
масс и зарядов.
Таким образом, из всего вышеприведенного следует, что в рассмотренных
системах, представляющих отдельные элементарные частицы, могут существовать по несколько
инвариантов как для массы, так и для заряда. Кроме того, имеется некий элементарный
флюид - не проявленное вещество - в виде частиц мнимых масс и зарядов - квазичастиц,
с помощью которого возможна передача возмущений посредством самой среды на уровне элементарных
актов.
На
этом, думаю, достаточно. В следующем выпуске я продолжу изложение подобного материала.
